[最新] √計算 中学 339047-計算 中学生 算数
計算:分数の掛け算、割り算 計算:文字を使った式 図形:円の面積、 角柱及び円柱の体積 中学校で習う算数の内容一覧 中学1年生 数:負の数 中学2年生 計算:文字を用いた式の四則計算 図形:平行線や角の性質 中学3年生 数:平方根(√) 計算:二例題8 次の数を、√ =の形で表しなさい。 ① 3 √5 ② 3√7 例題9 次の数を、 =√ >の形で表しなさい。 ① √12 ② √18 ③ √ ④ √24 例題10 次の計算をしなさい。 ① 2√53√6 ② 7√5 平方根はこれで完璧! 平方根の定義からルートの計算、近似値の問題の解き方まで 平方根という分野は中学三年生にとっての鬼門です。 ただ、これがなぜ中学生にとって難しいとされるのかという点については、少しだけ誤解があるようです

中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ
計算 中学生 算数
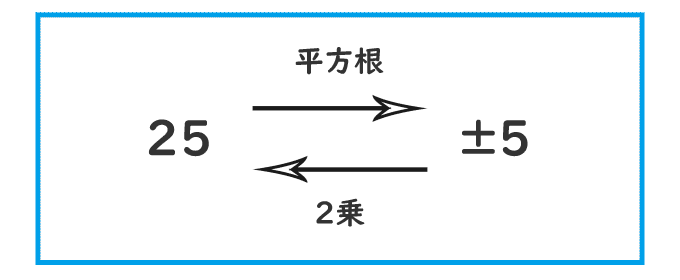
計算 中学生 算数- 平方根 √ とは何か? 計算方法・覚え方・どう役に立つのかを解説 ある数 a を 2 回かけ算することを「 2 乗する」と言い、 a 2 と書きます。 となります。 これに対して、「 2 乗すると x になる数」のことを「 x の平方根」と言います。 平方根は、英語 計算がややこしい数字も出てきますよね! 今回はその計算がややこしい数字と√(ルート)関係を解説します!! 計算がややこしい数字と√(ルート)の関係とは? まず、なぜ4や9を計算しやすい数と言ったかというと、 それは、 4も9も整数を2乗した数 だ
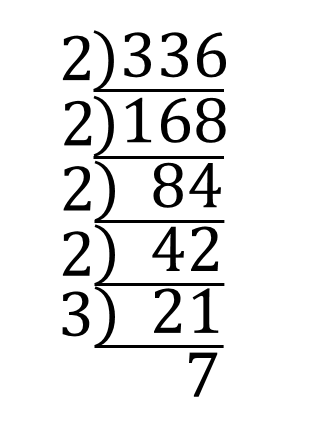



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ
計算式で表すと、次のようになります。 √とは「二乗すると、なかの数字になる」という意味の記号です。 中学や高校での数学の授業は、「すでにわかっている内容を学ぶ」ことになりますが、元々数学は「なぜこのような結果になるのだろうか√+2 −√ √+5 √−3 √+√√−√ 6 √+4 √−2 √√+2 √√+√ √√ /10 −2 √√−2 点 √+3 √− 平方根 平方根の計算1 無料で使える中学学習プリント ルートの分数計算、問題解説で完全マスターだ! ←今回の記事 整数部分、小数部分の求め方! 分数の場合には? 中3の数学で 「平方根」 の計算を学習します。 平方根というよりも 「√(ルート)」 と表現した方が、数学っぽいでしょうか。 この平方 平方根 いろいろな計算 平方根の
1年 文字式の計算2(加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5(3)解答(0,4)→(0,4)または(0,4) 1年 文字式の計算3(乗除) 答3③9c誤→49c正 1年 文章を等式にする 答(9)12x→ 9 2 x 1年 方程式計算4 ⑪右辺5/6→5/6xまず、1√2=Aと置きます。 そうすると、 (A√3)^2× (A√3)^2 = { (A√3) (A√3)}^2 = (A^23)^2 ここで、Aを1√2に戻します。 { (1√2)^23} = (12√223) = (2√2)^2 =8 となります。 ^2は二乗という意味になります。 回答する √の計算 (中学3年) MathQ https//mathq2ndcom平方根の加法減法3 (分数) √の中の数が異なる場合でも 分母を有理化し、√の中をできるだけ簡単にすると計算できることもある。 解説動画 ≫ つぎの計算をせよ。 14 7 57 12 2 3 76 16 5 2 90 14 757 = 14× 7 7 × 757 = 14 7 7 57 = 2757 = 37 分母に√があるときは
√8 12 6 √24÷√8×√3 √ √24÷√3 √6× 2√ √2×√3 √3×√75 No2 /10点 平方根 平方根の計算 乗除2 無料で使える中学学習プリント 中学数学 x=1/√3(x+2)の途中式・答えを教えて頂きたいです。 最初の計算問題を不安で何回も見直ししてしまい前に進めません、、、また、今回は証明と確率なので時間に余裕を持ちたいです。 こういう時は見直しを後回しにして次の問題にどんどん平方根 求め方(ステップバイステップ): 平方根の計算の準備をするには、基本的な完全な平方根を覚えておく必要があります。 1、4、9、16、25、100のsqrtは、1、2、3、4、5、および10です。 √25のsqrtを見つけるために、見てみましょう! √25=√5* 5 √25




かっこのルートを二乗する問題 を外すだけなので簡単 中学や高校の数学の計算問題
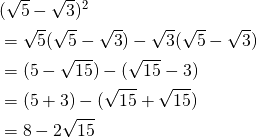



ルート 根号 の計算方法をマスターしよう スタディクラブ情報局
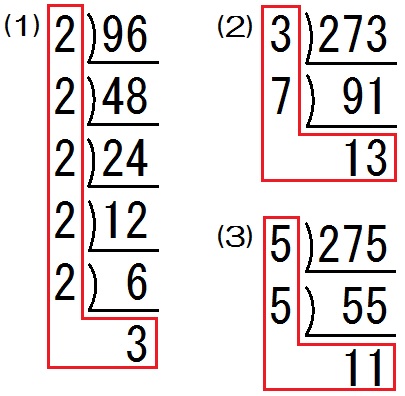
√100以上 中学 数学 平方根 1758中学 数学 平方根 難問 をフォローをしませんか 中学数学「平方根」のコツ③ 素因数分解/ルートを簡単にする計算 中学数学のつまずき解消をめざすこの連載。 中3「平方根」の3回目は 素因数分解 と ルートを簡単にする √を含む因数分解 √が入るあらゆる計算問題を完璧にしておきましょう。 2次方程式 中学3年の範囲ですね。 ちなみに高校数学で最初に学習するのは、 「式の展開」と「因数分解」です。 "高校が始まる前に必ずやるべきこと" 「解の公式」を使った計算 単元 平方根,根号をふくむ式の計算,有理数と無理数,平方根の利用, 「√の計算方法をまとめてみました!予習・復習に使ってもらえたら嬉しいです!」, 学年 中学3年生, キーワード 平方根
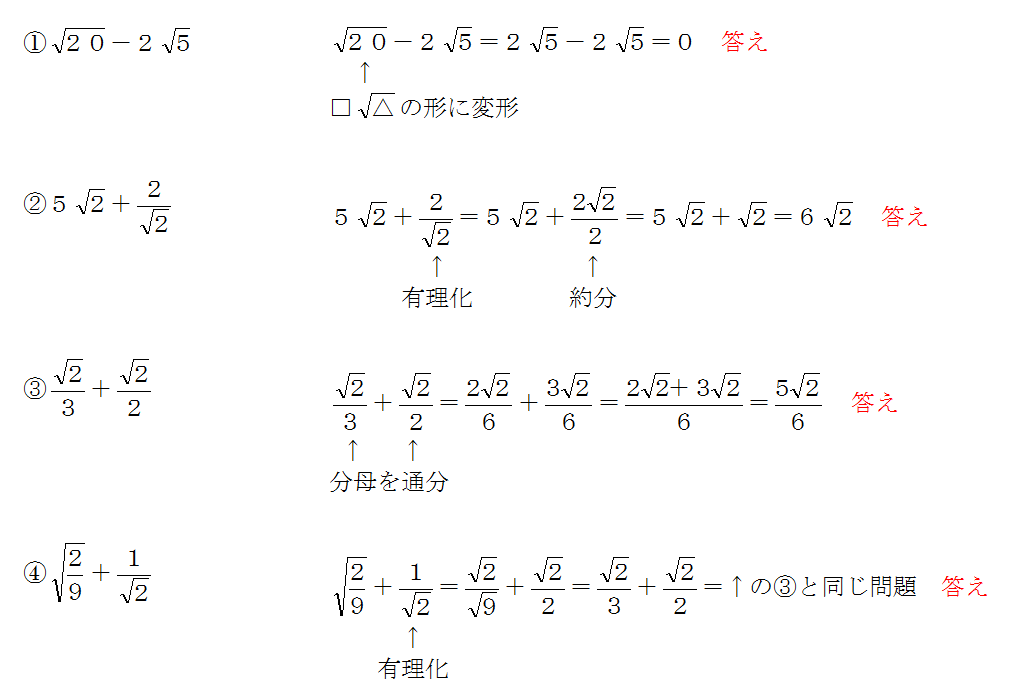



平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




平方根 ルート の重要な計算方法まとめ 数学fun
中学数学公式一覧 Ver112 (21 年5 月6 日作成) 1 計算の公式 11 交換法則・結合法則・分配法則 加法の交換法則 ab = ba 加法の結合法則 abc = (ab)c = a(bc) 乗法の交換法則 ab = ba 乗法の結合法則 abc = (ab)c = a(bc) 分配法則 (ab)×c = c×(ab) = acbc 12 等式の性質 A = B が成り立つとき、 和 AC = B C 差 A−C 「 √の計算です。 予習復習に使ってもらえたら 嬉しいです🙌🏻 良ければ♡・💬・👤 よろしくお願いします🦥 リクエストありがとぉぉ♡ これで良かったかな?😿 」, 学年 中学全学年, キーワード √の計算,√,有理化,心桜次の計算をしなさい。 ① √3 h√5 ② √6√7 ③ √10 j√2 ④ √ 5 8 √ ;
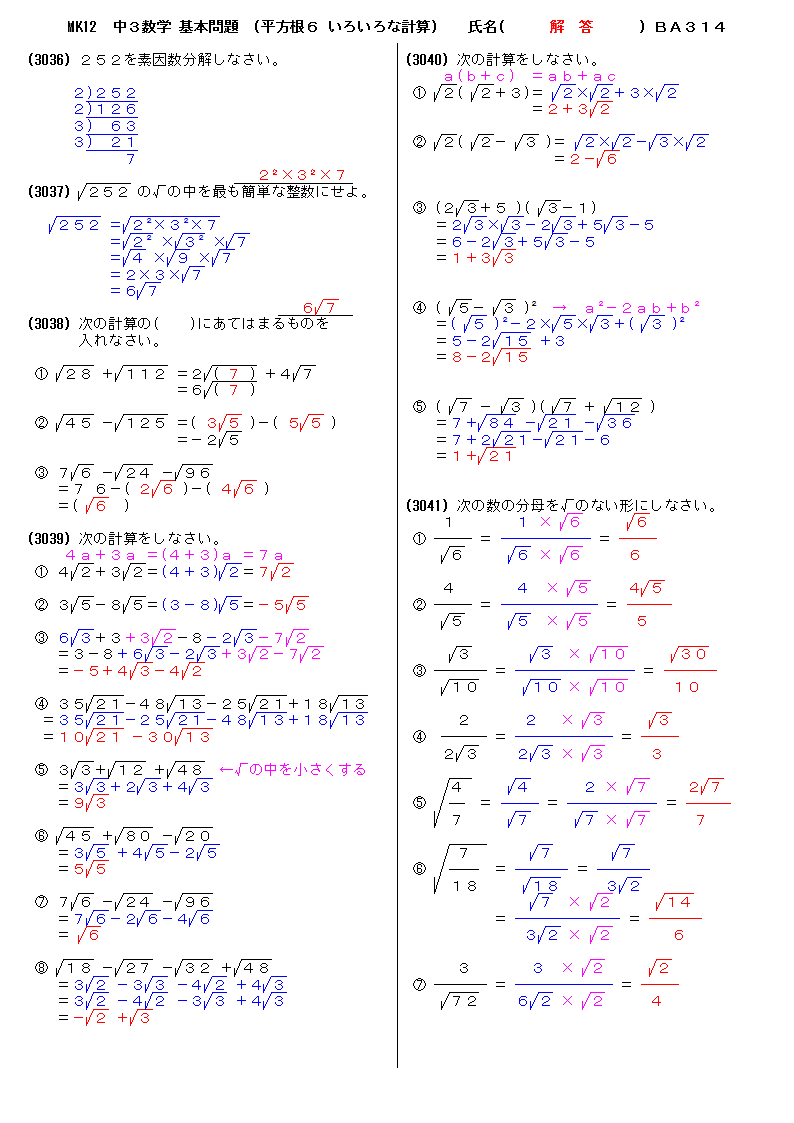



無料 中3数学 基本問題 解答プリント 314 平方根6 いろいろな計算
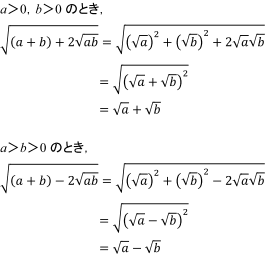



2重根号の計算 数学 苦手解決q A 進研ゼミ高校講座
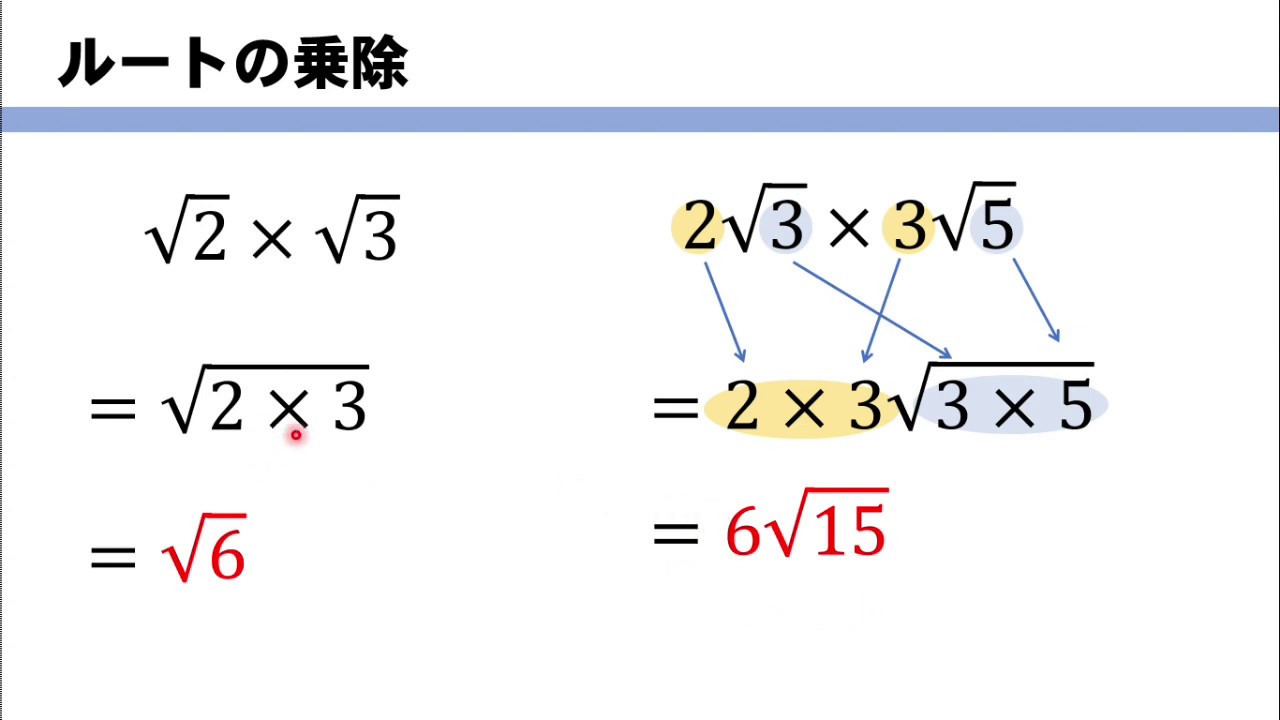
中学2年生 数学 式の計算 単項式の計算 乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生 1式の計算 カレンダーの中に潜む秘密を探ろう 1 2 年 ねらいと評価 単元の目標 カレンダーの中に潜む秘密(数の関係)を発見し,文字式を利用し ルート(√)の足し算、引き算、掛け算、割り算は、中学3年生で習う数学です。 足し算、引き算、掛け算、割り算の計算は以下のようになります。 足し算:√2+√2=2√2 引き算:2√2ー√2=√2 掛け算:√2×√2=2 割り算:2√2÷√2=2 とにかく覚えてしまえば良い? それ – √3 × √5 が計算できそうだ。 平方根の掛け算では「√の中身」を計算してもよかったよね?? だから、 – √3 × √5 = – √15 になるね。 あとは左の足し算。 2√2;




ルート 平方根 の計算




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
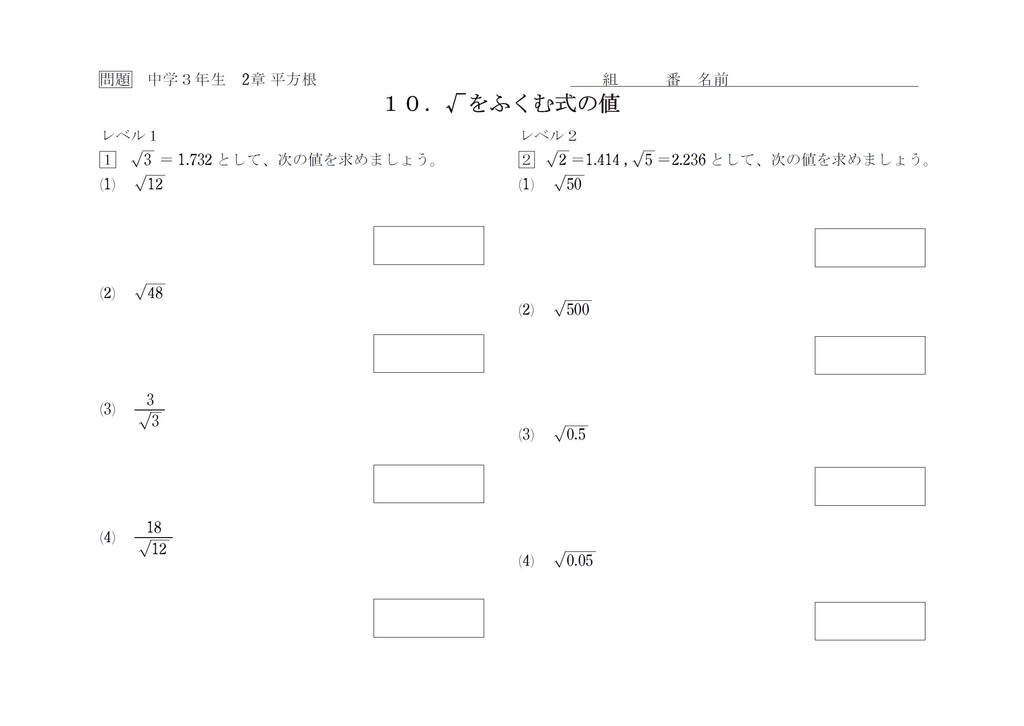
中学の数学・方程式が超わかる本 びっくりするほど説明がていねい! 飯田圭一 価格 1650 円楽天で詳細を見る 二次方程式のテクニック 1⃣ ax^2bxc=0(a≠0)でbが偶数のときに使えるテクニック b÷2=b'とすると、下のように解の公式を使った計算を簡単にできる。 x=b'±√(b'^2-ac)/a 2⃣ 二次 中学数学「平方根」のコツ⑤ 平方根の近似値・式の値 中学数学のつまずき解消をめざすこの連載。 中3「平方根」の5回目は、 近似値および式の値という応用問題 を解説します。 つまり、こんなの↓ 例1) , として、次の値を求めよ。 ① ② ③ ④ 例2平方根√(ルート)の重要な計算方法まとめ 管理人 3月 4, 19 / 6月 18, 前回、 平方根の意味や性質、値の求め方 などを解説していきましたが、今回は平方根の計算について見ていきます。




中3数学 ルート 平方根 の計算方法における3つのコツ Qikeru 学びを楽しくわかりやすく




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ
√の 外側ももちろんそのまま 掛け算割り算できます。 (7) 3 √ 3 × 2 √ 3 = ×√(18 (50×18)=√900 2 ×10 2 この問題の時、先に平方根を簡単にしてから計算することもできます。 2 2 =(√() √の中の数字が大きすぎる場合は、 先に平方根を簡単にしてから √の足し算・引き算は、√の中の数字が同じ数のもの同士で計算する! √の足し算・引き算の計算方法は、 中学2年生の時に習った単項式・多項式の計算方法とそっくりで意外と簡単 なんです! 多項式の計算は、 √ 中 1 音楽 中学 音楽 テスト 音符 ヴィヴァルディ 四季「春」 横浜市泉区 たちかわピアノ教室💛SuZu💛 中1音楽 音符の計算 中学音楽定期テスト対策まとめ 問題付き (前期) 2 4 *音楽*~6割がた中1まとめ~ 124 5 翔虹⚡︎ 中2 音楽 2学期 期末考査対策




1 2乗って何 どうしてそれがルート 平方根 になるのか 数学の面白いこと 役に立つことをまとめたサイト



1
A√bの形に変形するやり方とは? 平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは? 分母の有理化のやり方はこれでバッチリ! ルートの計算方法まとめ!問題を使って徹底解説! ルートの分数計算、問題解説で完全マスターだ!「√の中が小数になる問題」 は、 上記ページの続きになるので、 "順番に練習すれば、実力アップする" という数学のコツを意識してくださいね! √2÷ 、√÷ を作ろう では、上記ページを しっかり理解した中学生向けに、 続きを説明していきますね。 計算や図形、関数など数学にはさまざまな公式が登場します。 √a×√b=√ab などです このほかにも計算で使う公式には二次方程式の解の方式があります。 中学3年生になると三角形や直角三角形の合同条件が出題されます。




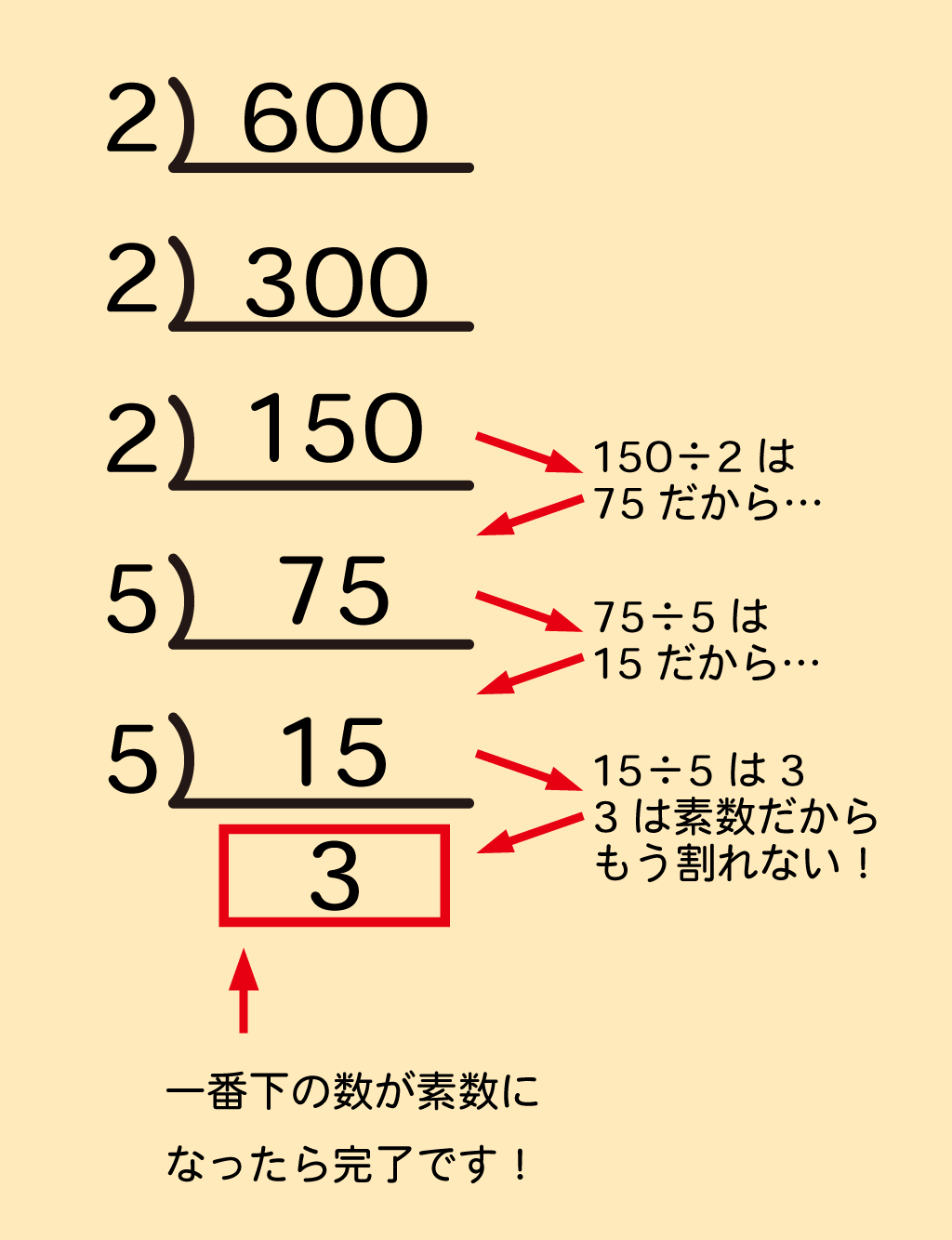
中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師
しかし、√2, √3, √5などは少数点以下が何桁も続く数字になります。 その 少数点以下を省略して「だいたいこれくらい」としたのが近似値です。 √2, √3, √5, √7, √8は良く出てきて答えの確認にも使うことが出来るので近似値を覚えておきましょう!



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




中学生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



3




2倍時短 分母の有理化の無駄を省けば計算スピードに差が付く 超わかる中学数学 Youtube




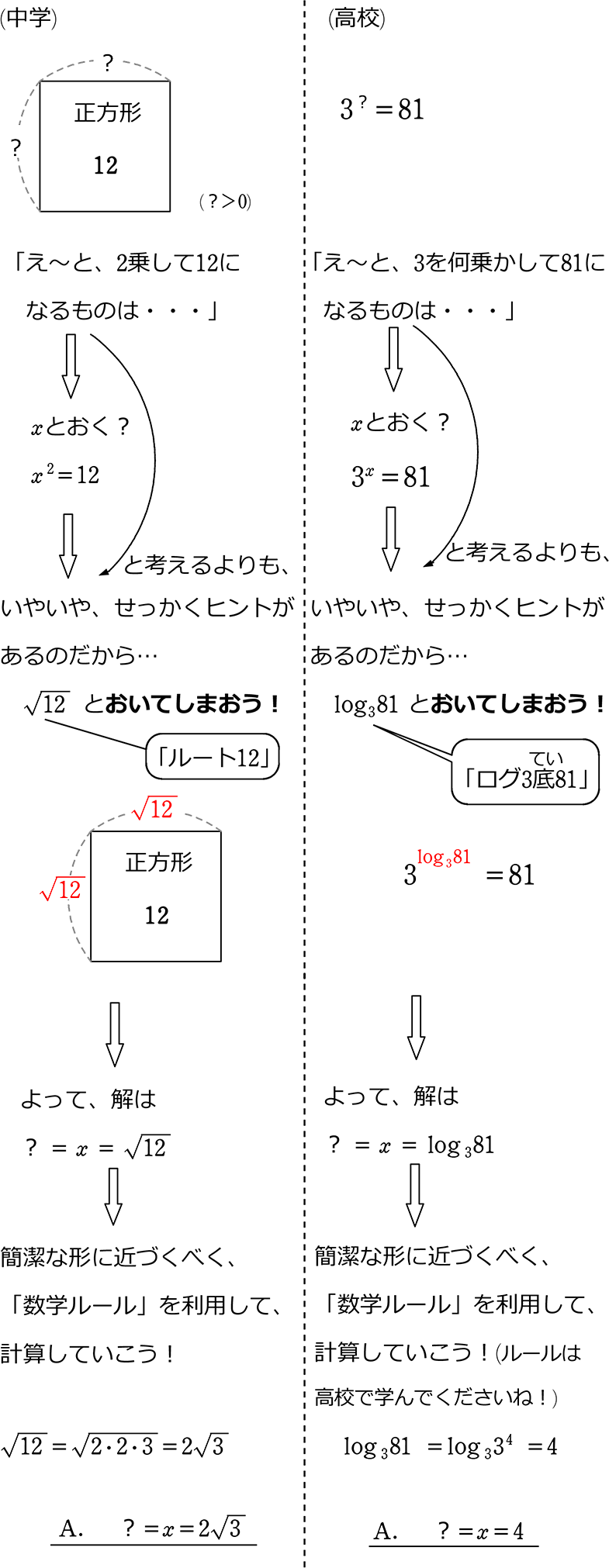
高校数学 指数計算 中学数学 高校数学




ルートの分数計算 問題解説で完全マスターだ 数スタ
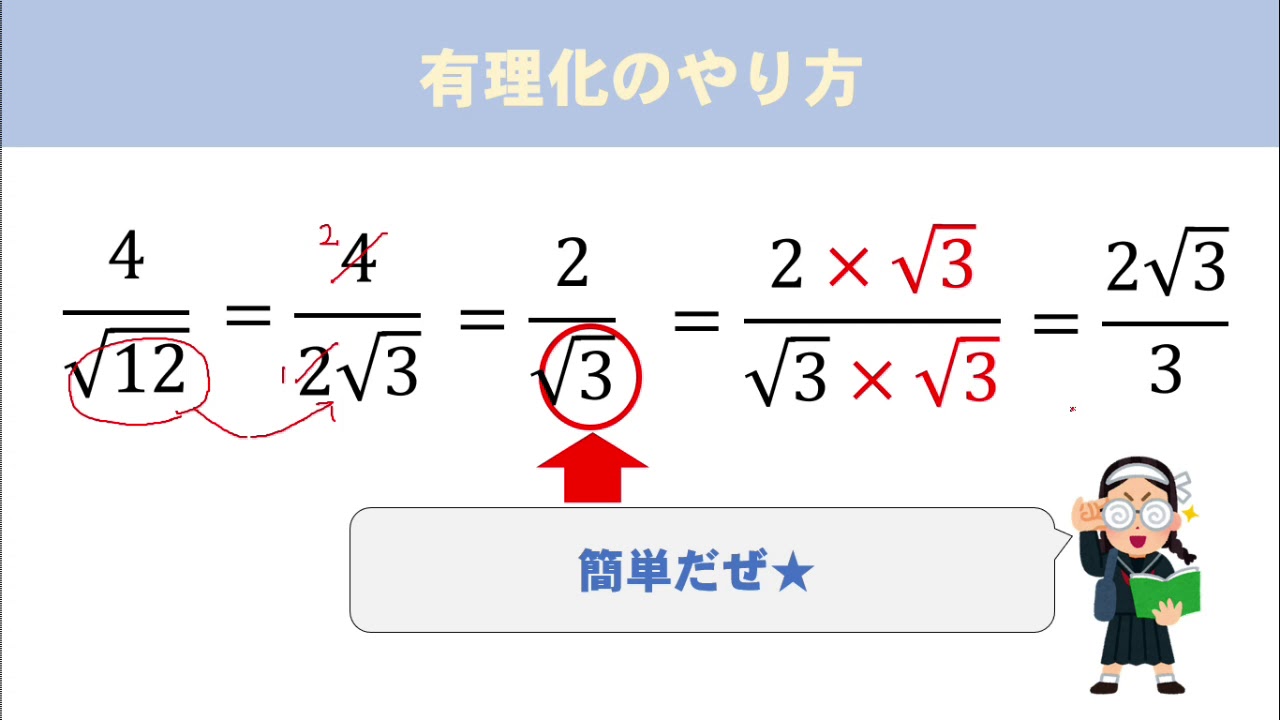



平方根 分母の有理化のやり方はこれでバッチリ 数スタ
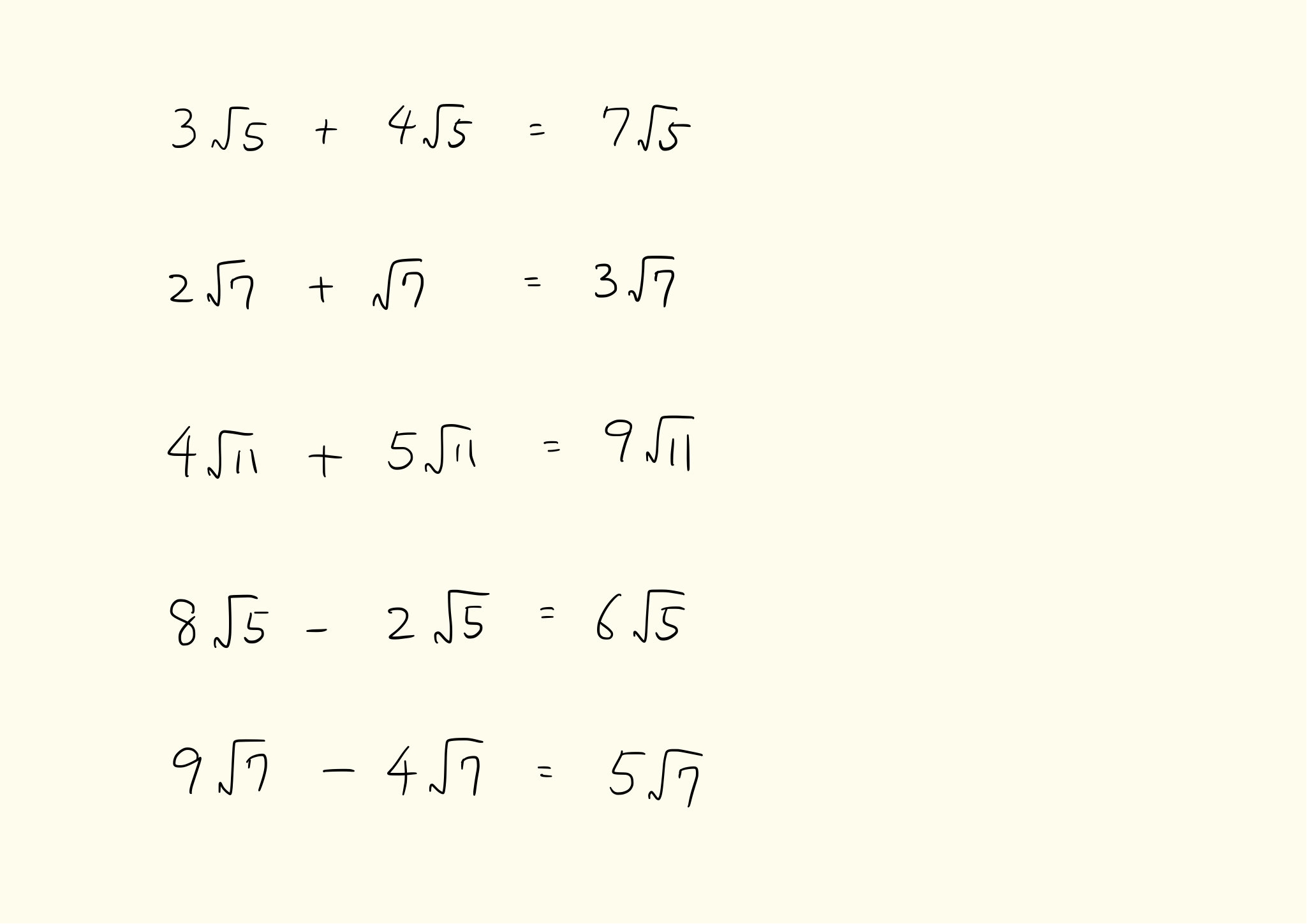



平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




平方根の問題の解き方 6パターン 数学fun




高校数学 数 13 ルート シリーズ 有理化編 Youtube
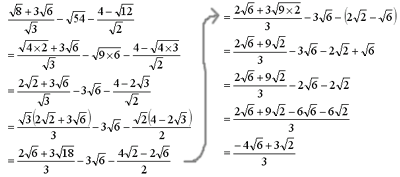



中学の数学 ルートの計算方法って Sakura Scope



中学校3年生数学 平方根の性質 成果主義 Itto個別指導学院 長野市の学習塾




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学 中3 23 ルートの問題をつめこんでみた Youtube
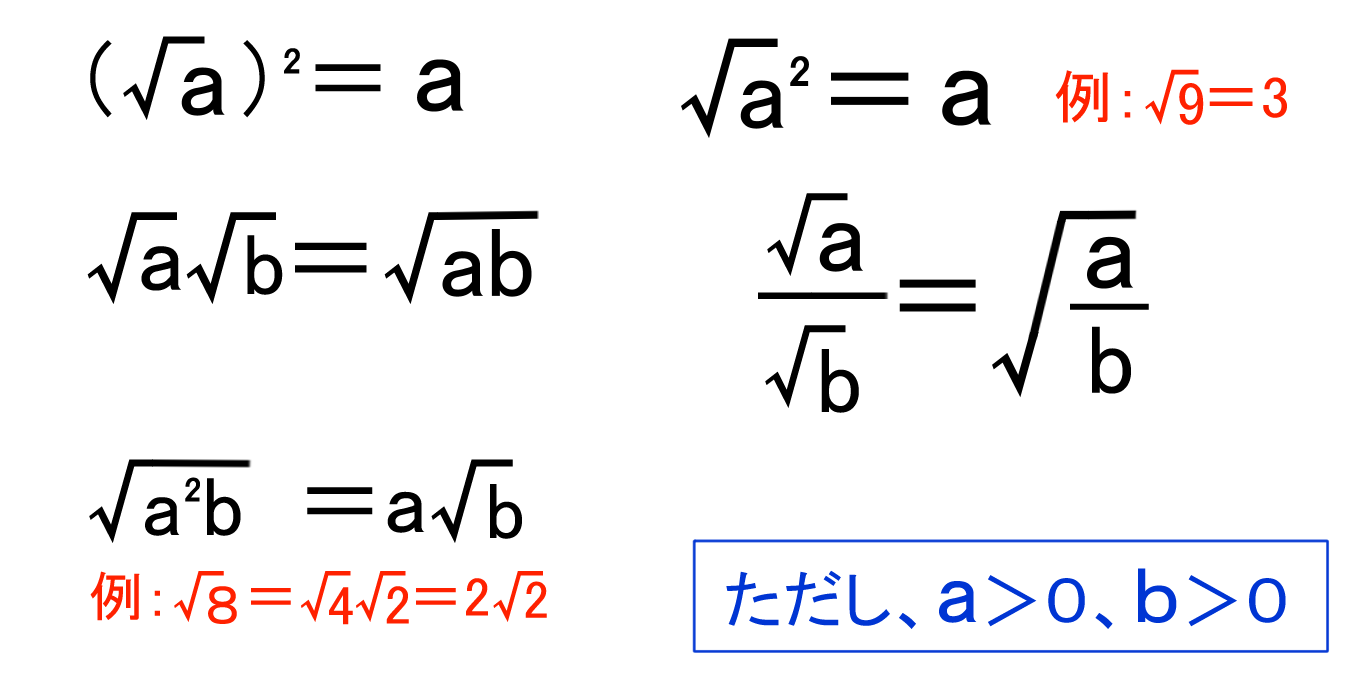



平方根 1 基本のルール バカでもわかる 中学数学




式の計算 あんのん塾




平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook




平方根 ルート の重要な計算方法まとめ 数学fun



中学数学 平方根 のコツ 素因数分解 ルートを簡単にする計算




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




3乗根を簡単に暗算で計算できてしまう方法 数学の面白いこと 役に立つことをまとめたサイト



中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




中学数学 式の計算の利用 ママ塾ノート




中学3年生 数学 平方根の加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学の数学 平方根 を理解して受験を乗り切ろう 札幌市 学習塾 受験 チーム個別指導塾 大成会




中学数学 平方根 のコツ 素因数分解 ルートを簡単にする計算




の四則計算 Youtube




無料 中3数学 基本解説 解答プリント 314 平方根6 いろいろな計算




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく




数学 中3 21 ルートの計算のまとめ Youtube




中学数学 平方根 のコツ 有理化 加減乗除 展開




平方根 1 基本のルール バカでもわかる 中学数学




ルートの四則演算 計算する順番に注意しよう 中学や高校の数学の計算問題




中学2年数学 式の計算 単項式の掛け算の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト



中3 平方根10 近似値 中学数学の勉強に




平方根 ルート の重要な計算方法まとめ 数学fun




平方根の公式 中学生が覚えるべき掛け算と割り算の公式 中学や高校の数学の計算問題




中学校3年生数学 平方根の性質 成果主義 Itto個別指導学院 長野市の学習塾
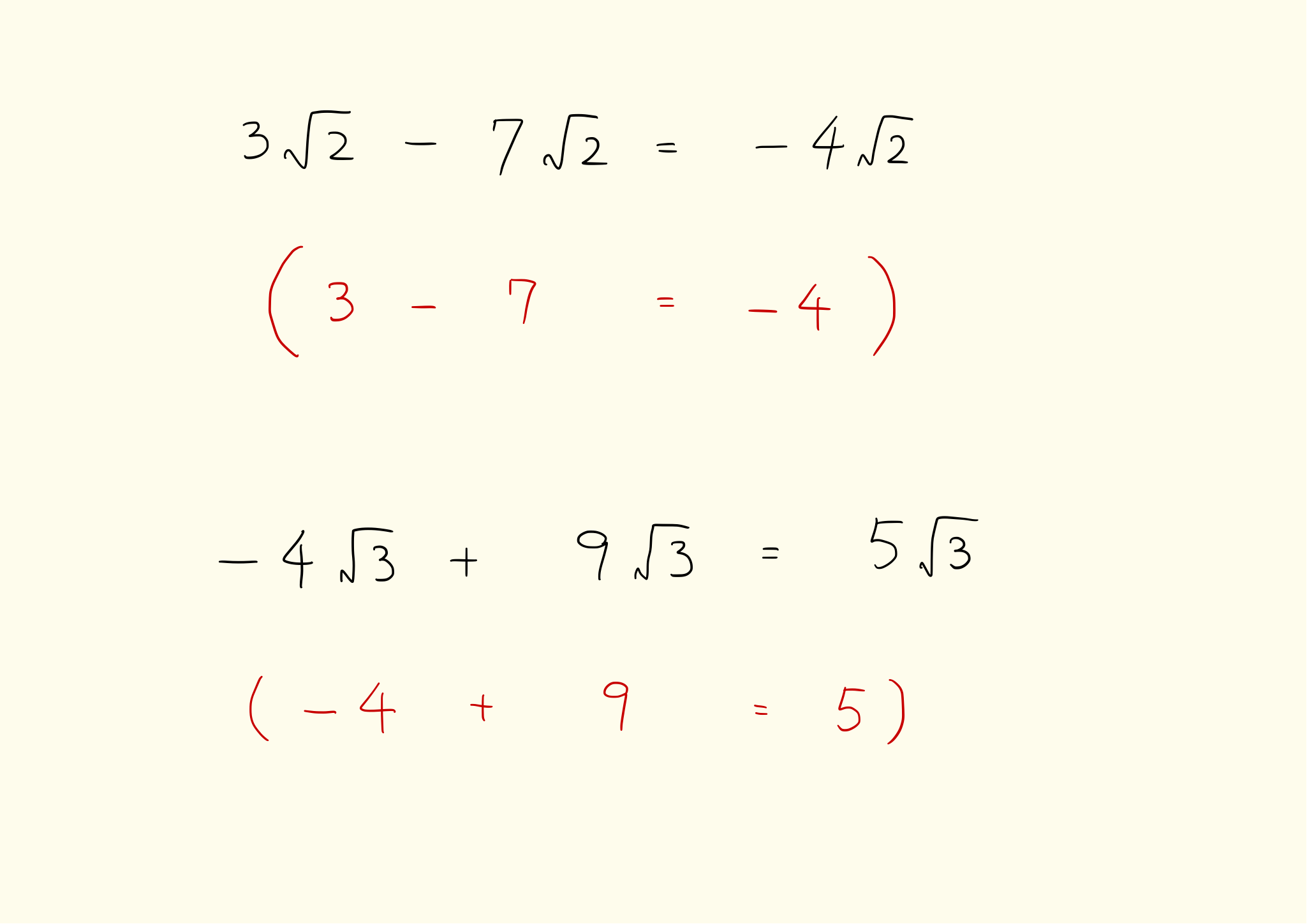



平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




中3 平方根7 乗除1 中学数学の勉強に




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



中学数学 平方根
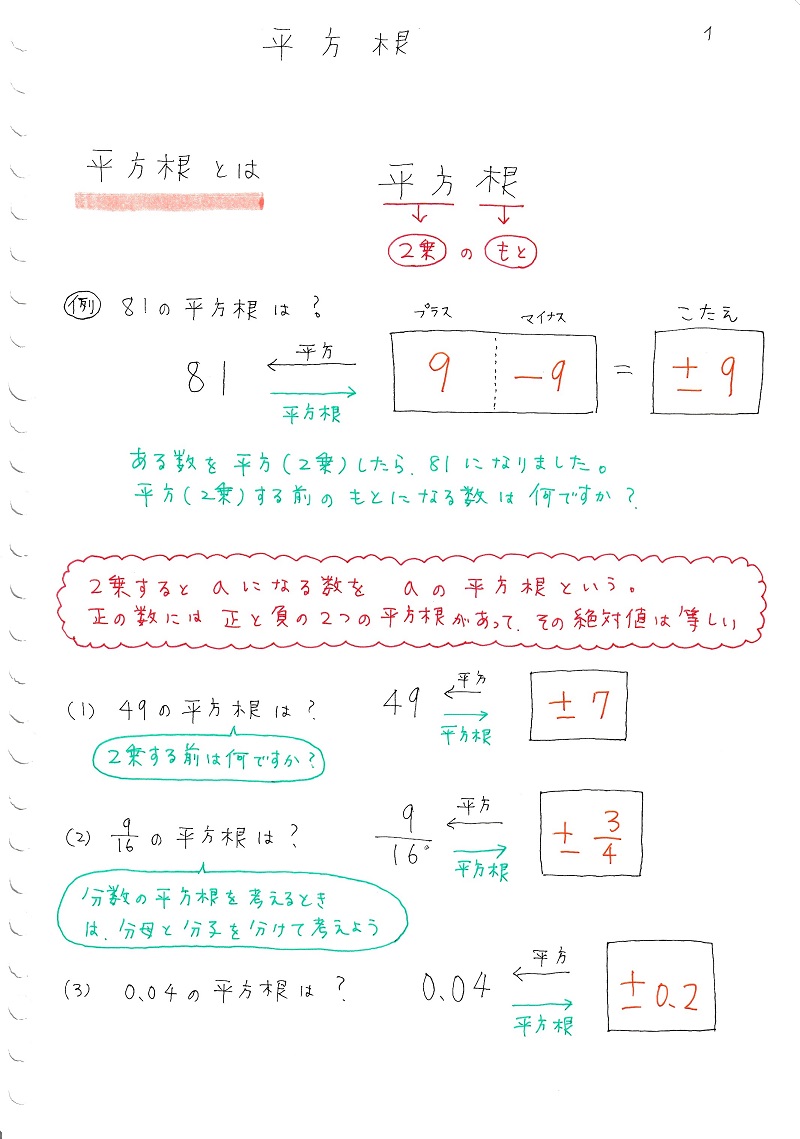



中学数学 平方根 ママ塾ノート




平方根の応用 無料で使える中学学習プリント
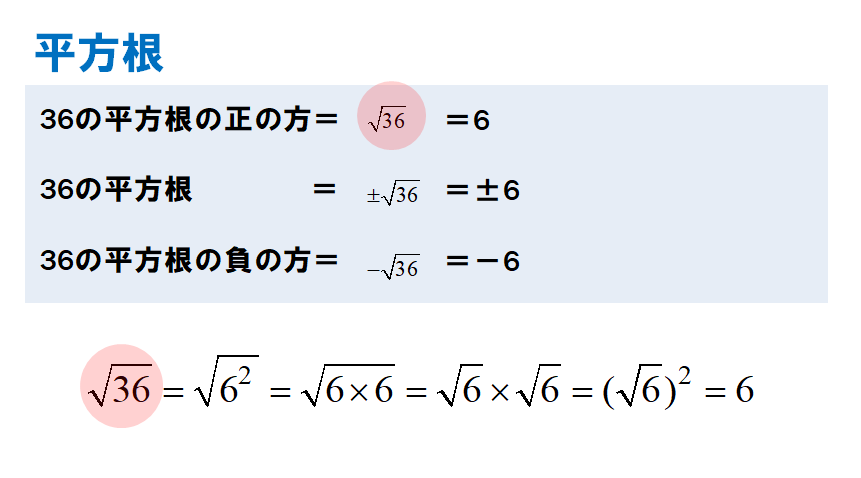



中3数学 平方根の性質の定期テスト対策問題 Examee



1




数学 中3 19 有理化 Youtube
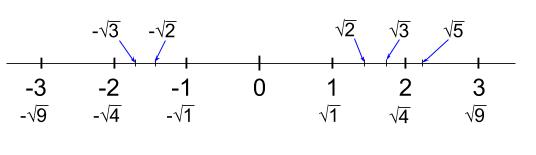



中学数学 平方根の導入 その2 中学数学の無料オンライン学習サイトchu Su




中学数学 平方根のひみつ 都立高校入試で成功する方法




高校数学 N aの計算公式 映像授業のtry It トライイット




中学数学 多項式の計算 ママ塾ノート




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中学数学 平方根の利用 ママ塾ノート




中学生の数学で習う平方根 ルート の計算や問題の解き方を理解しよう




整数をルートにする方法 5秒で計算できる簡単な問題だ 中学や高校の数学の計算問題




中学3年の数学 動画 ルートの計算のまとめの問題 19ch




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
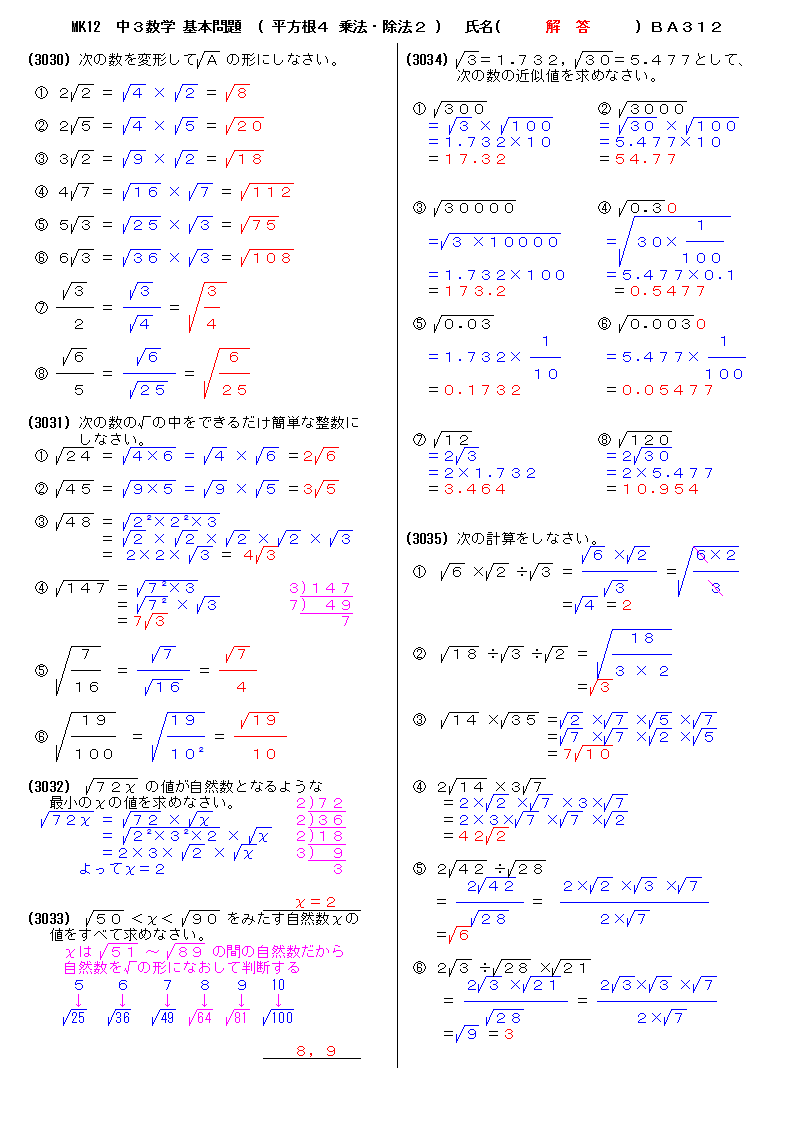



無料 中3数学 基本問題 解答プリント 312 平方根4 乗法 除法2




ルートの応用問題 を変形して 計算できるようにする 中学や高校の数学の計算問題
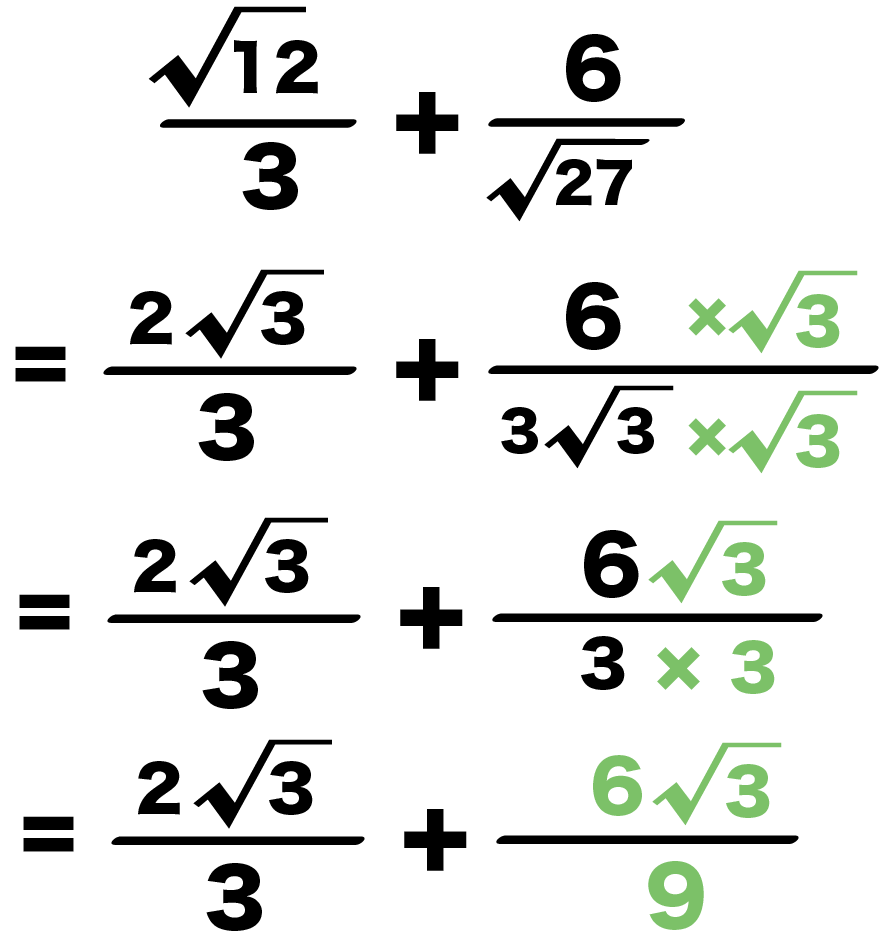



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




中3数学 ルート 平方根 の計算方法における3つのコツ Qikeru 学びを楽しくわかりやすく



2




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット




平方根の乗法 中学校3年の数学 2 3 6 身勝手な主張




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット
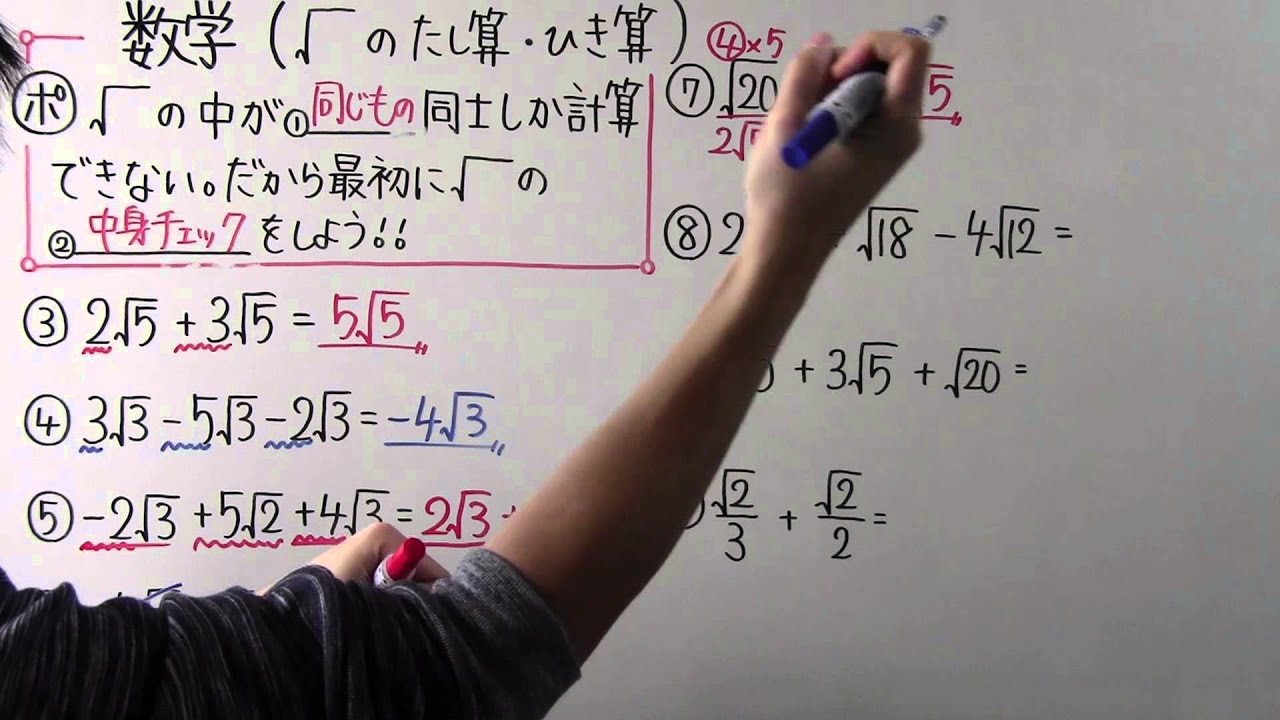



数学 中3 ルートのたし算 ひき算 Youtube




ルートの足し算のやり方 簡単すぎる例題問題を解いてみよう 中学や高校の数学の計算問題




平方根の乗法 身勝手な主張




平方根 ルート の重要な計算方法まとめ 数学fun
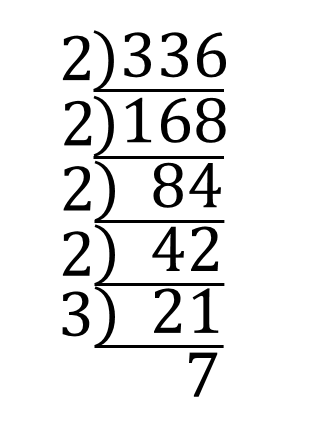



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ
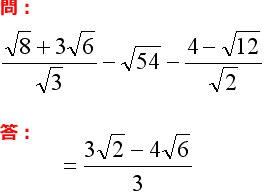



中学の数学 ルートの計算方法って Sakura Scope



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




ルート をマスターしよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ



中学の数学 ルートの計算方法って Sakura Scope



3




中3数学 ルート 平方根 の計算方法における3つのコツ Qikeru 学びを楽しくわかりやすく
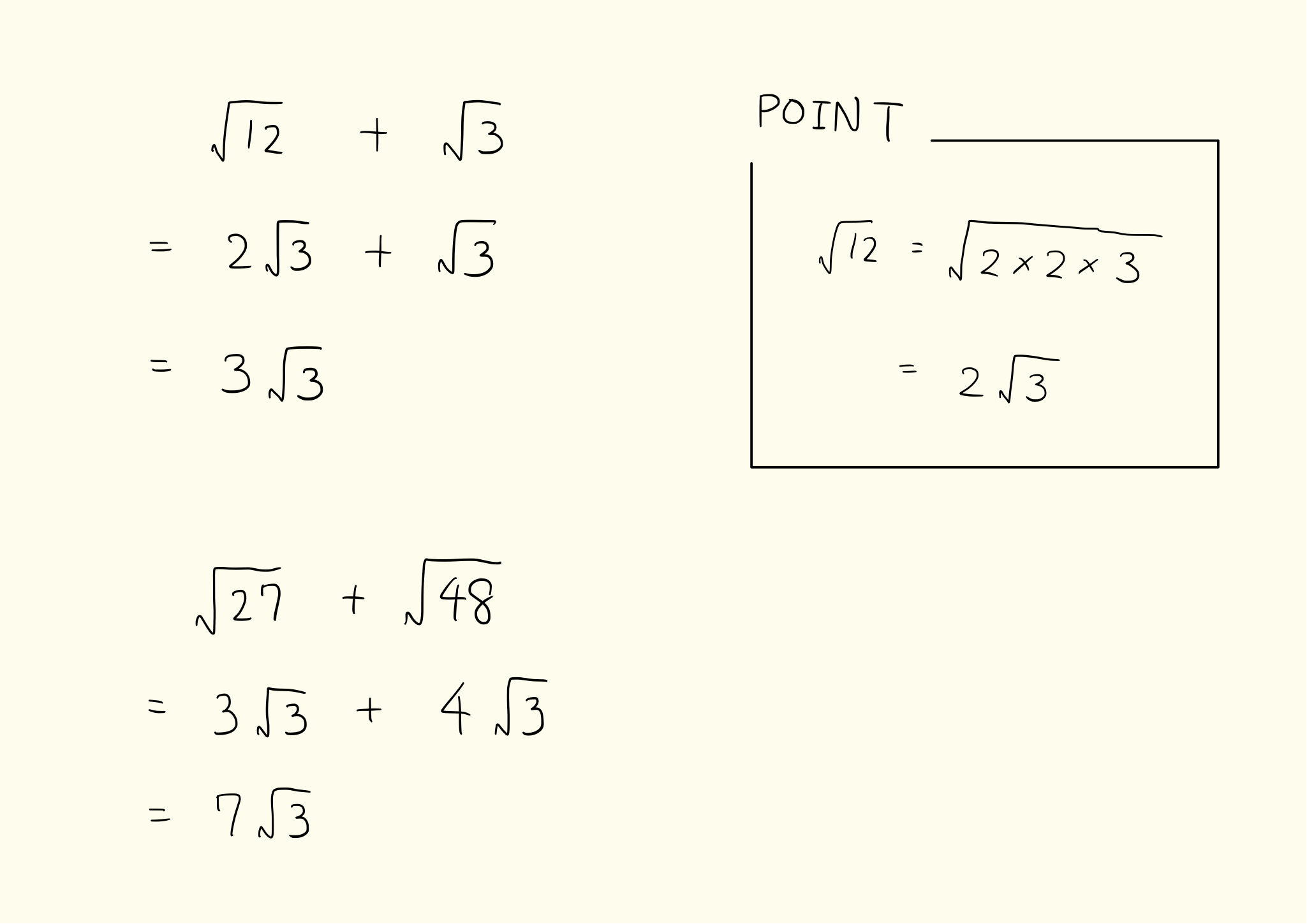



平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook




高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド
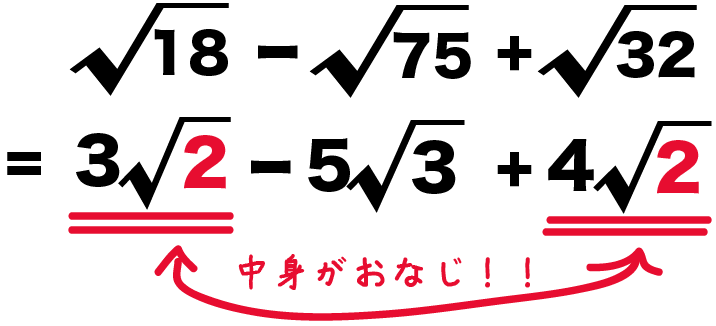



平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




平方根 ルート の重要な計算方法まとめ 数学fun
コメント
コメントを投稿